Multiple Correlation

Correlation between 3 variable
It is used to measure the degree of association of two or more quantitative variables
It mainly describes the relationship between two variables and how they relate to each other.

Usually, we use the correlation between two variables but for the current situation of obesity, inactivity, and diabetes data we need to use the Correlation for three variables

Given variables x, y, and Z, we define the multiple correlation coefficient as

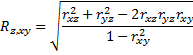
Here x and y are viewed as the independent variables and Z is the dependent variable.
If we find the Correlation between two variables, we can eliminate one of the variables

Project

First, I analyzed the data of three different sheets and tried to merge the three data into one so that it was easy to interpret, I sorted for “FIPDS” or “FIPS” since I considered as the primary key

After I merged those data, I tried to analyze the data and tried to form a relationship between inactivity and diabetes
Plotting the graph for these two where diabetes in the x-axis (Independent variable) and inactivity in the y-axis (Dependent variable)

After this, I tried to calculate the Mean, median, mode, variance, and Standard deviation for the above
For the next step, I’ll try to calculate the relation for all three variables and plot and analyze the graph

What is the P-value ?

The p-value is a measure of the observed value of the test or evidence against the null hypothesis

To calculate the P value
H_o : µ = µo
Ha : µ > µo

The smaller the p-value, the greater the evidence against the NULL hypothesis

If we have a significance level of alpha
We can reject H_o if the P-value is ≤ alpha

If we do not have a given significant level, then we cannot reject null hypothesis

In short

• P-value < 0.01
  Very strong evidence against H_o
• 0.01 < P-value < 0.05
  Strong evidence against H_o
• 0.05 < P-value < 0.1
  weak evidence against H_o
• P-value > 0.1
  little or less evidence against the H_o Heteroscedasticity Breusch-Pagan Test

On linear regression, the residuals are distributed with equal variance at each level of the dependent variable Y

So Heteroscedasticity means the Differently scattered or the spread of the residual over the range is More and Homoscedasticity means the Same scatter

The Breusch-Pagan Test, in which the null hypothesis is that Homoscedasticity is present and against the alternative Heteroscedasticity is present

H_o : Homoscedasticity is present (Error on variance are all Equal)

Ha : Heteroscedasticity is present (Error on variance are NOT Equal)

how do we calculate or compare

1. Get the residual
2. Square the residual and calculate Pearson’s R2
3. Calculate the probability P for the Chi-Squared distribution

If P is small Reject the hypothesis meaning
If the calculated chi-square exceeds the critical value or significant value

which helps us to conclude Heteroscedasticity is present in the model